Full Unit Circle Chart
Full Unit Circle Chart – The unit circle is the golden key to truly understanding trigonometry. Like many concepts in mathematics, its simplicity makes it beautiful.
The measurements of sin, kos and tan become clear when you see them in the graph. Take some time to consider their ideas.
Full Unit Circle Chart
A circle clearly shows the trig function because the radius is 1. The bottom does not change the sin, cos, and tan values.
Solved Fill Out The Unit Circle Completely. Express The
A little time to remember them now will save you a lot of time, doing your job in the future.
Remembering may seem painful, but don’t worry, there are tricks to help. Let’s start with sin values.
It’s easy to remember this by thinking of a stop sign, and lettuce. See where this is going?
Unit Circle Degrees
Tan also leads to a good model, although it doesn’t have 0° and 90° like sin and cos.
Put all these together and you get a table of specific trigonometric values, or a round table:
You might like it, because you can understand it, even in the middle of the exam!
File:unit Circle Sine Cosine.svg
Next, use SOH CAH TOA in the triangle. Remember that each interior angle of an equilateral triangle is 60°, so the bisected angle is 30°.
The values of sin, cos and tan remain the same in each quadrant, but the sign changes according to the quadrant in which the angle is located.
And connect them all together. This leads to this very useful diagram. Click/tap the image to upload a printable PDF file.
Geyer Instructional Products 172898 Unit Circle Dry Erase Magnet: Amazon.com: Industrial & Scientific
There it is! Values of pi, π, are called radians. They have a special relationship with the circle and are the next step in controlling the circle. The circle can be used to determine the right triangle ratios known as sine, cosine, and tangent. © HowStuffWorks 2021
You may have an intuitive idea of what a circle is: the shape of a basketball hoop, a wheel, or a quarter. You might even remember from high school that a radius is a straight line that starts at the center of a circle and ends at its circumference.
A circle is a circle with a radius of 1. But it often comes with other bells and whistles.
Occult Unit Circle
A circle can be used to define the right triangle ratios known as sine, cosine, and tangent. These relationships describe the relationship between the angles and sides of a right triangle. For example, suppose we have a right triangle with an angle of 30 degrees, and the longest side, or bottom, is 7. We can use the predefined right triangle ratio to determine the length of two sides: the triangle. .
This branch of mathematics, known as trigonometry, has practical everyday applications such as construction, GPS, plumbing, video games, engineering, carpentry, and aerial navigation.
To help us, we will remember a trip to a single pizza palace. Take a moment to memorize the following until you can recite it without looking:
Graph And Formula For The Unit Circle As A Function Of Sine And Cosine
Imagine a whole pizza, cut it into four slices. In mathematics we call the four areas of a circle squares.
Fig. 2. Grouping of circles with the addition of fours. Square 1 is top right, square 2 is top left, square 3 is bottom left and square 4 is bottom right.
We can use the (x, y) coordinates to determine all the points on the outer edge of the circle. The x-coordinate represents the distance to the left or right of the center. The y coordinate represents the distance traveled up or down. The x-coordinate is the cosine of the angle formed by the point, the origin, and the x-axis. The y coordinate is the sine of the angle.
Free Free Unit Circle Practice Chart
In a circle, a straight line passing from the center of the circle will reach the edge of the circle at the coordinate (1, 0). If we go up, left or down, we will touch the circumference at (0, 1), (-1, 0) or (0, -1) respectively.
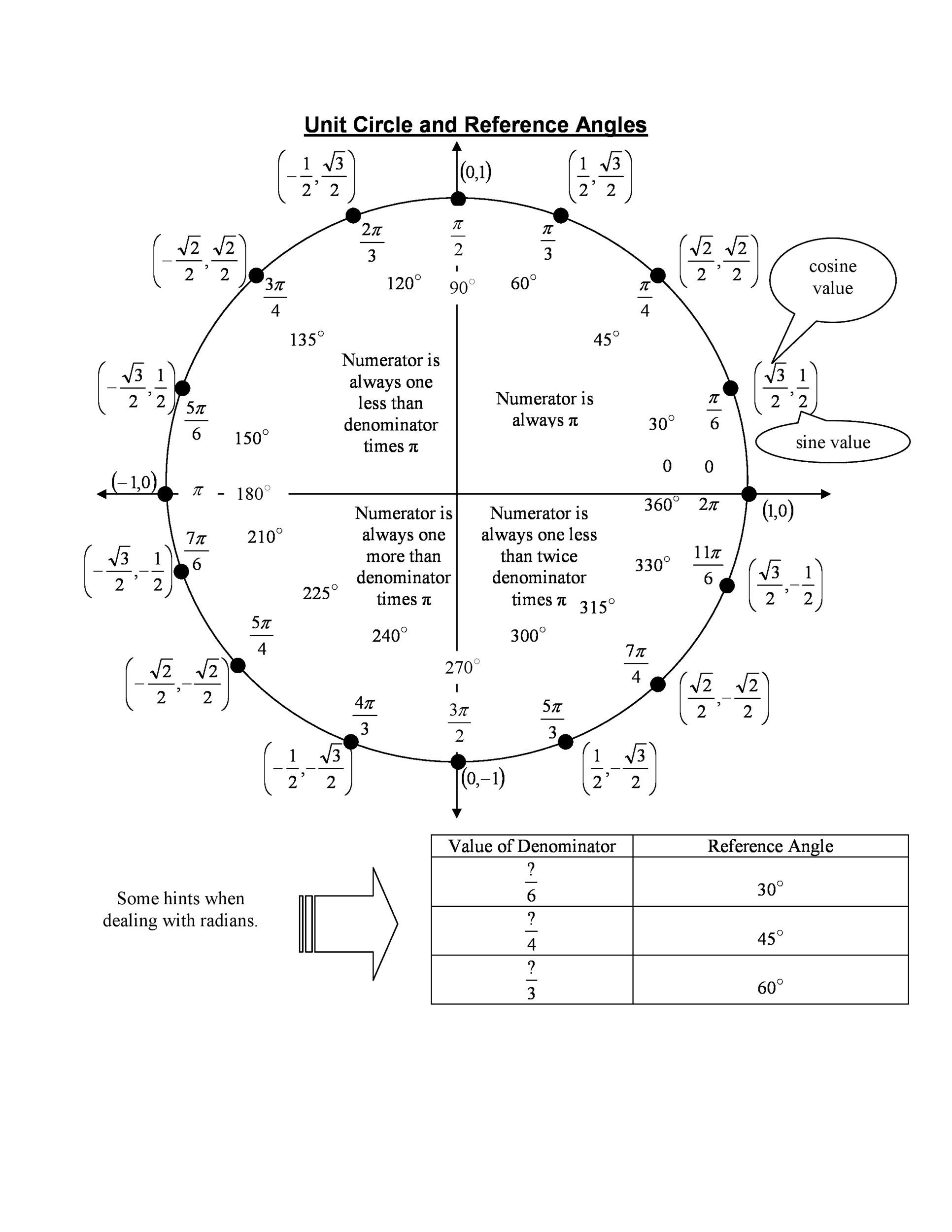
The four related angles (in radians, not degrees) all have a denominator of 2. (The radian is the angle formed when you take the radius and wrap it around a circle. Degrees measure angles by distance. A circle is 360 degrees or 2π radians).
The count starts at 0, starts at the coordinate (1, 0), and counts counter-clockwise by 1π. This process will produce 0π/2, 1π/2, 2π/2 and 3π/2. Simplify these parts to get 0, π/2, π and 3π/2.quad
Amazon.com: The Unit Circle Chart
Starting with “3 pies”. Look at the y-axis. Radian angles directly to the right and left of the y-axis have a denominator of 3. The remaining angle has a numerator that includes the mathematical value pi, written as π.
“3 pies for 6” is used to remember the remaining 12 angles in a regular circle, with three angles in each quarter. Each of these angles is written as a segment.
“For $6” reminds us that in each quarter, the remaining denominators are 4 and then 6.
Unit Circle Reference Chart
In square 2 (top left of the circle), put 2, then 3, then 5 before π.
The first angle in quadrant 2 is 2π/3. Add 2 in the numerator and 3 in the denominator to get 5. Look at the right angle in square 4 (the right side of the circle). Put that 5 in front of π. Repeat this process for the other two corners in quadrants 2 and 4.
We repeat the same process for quadrants 1 (top right) and 3 (bottom left). Remember that x is equal to 1x, π is equal to 1π. So we add 1 to all the denominators in quadrant 1.
Printable Unit Circle Charts & Diagrams (sin, Cos, Tan, Cot Etc)
The process of recording angles in degrees (not radians) is described at the end of this article.
The “2” in “square table 2” reminds us that the remaining 12 pairs of coordinates have 2 digits.
“Square” reminds us that every coordinate calculation has a square root. We start in quadrant 1 just to keep things simple. (Hint: Remember that the square root of 1 is 1, so these fractions can simply be 1/2.)
Amazon.com: Unit Circle With Radian Measures Cos Sin Recipe Math Poster Colorful Classroom Home Decor Wall Art Print Poster Chart Unframed
“1, 2, 3” shows us the sequence of numbers under each square root. For the x-coordinate of quadrant 1, we count from 1 to 3, starting at the top coordinate and working our way down.
The Y coordinate has the same number, but counts from 1 to 3 in the opposite direction, from bottom to top.
Square 3 inverts the x and y coordinates from square 1. All x and y coordinates are also negative.
The Circle Constant
As in quadrant 3, also in quadrant 4 the x and y coordinates are converted from quadrant 1. But only the y coordinate is negative.
Angles can be specified in degrees instead of radians. To do this, start at 0 degrees at coordinates (1, 0). Then add 30, 15, 15 and then 30. In quadrant 1 add 30 to 0 to get 30, add 15 to 30 to get 45, add 15 to 45 to get 60, and add 30 to 60 to get. 90.
We then repeat the process for the remaining quarters, adding 30, 15, 15 and 30 until we reach the end of the circle. Therefore, quadrant 4 will have an angle between 270 and 330 degrees (see Figure 10).
Labeling The Unit Circle Using Radians
At the beginning of the article we said that by means of a circle it is possible to find two unknown sides of a right triangle with an angle of 30 degrees, and the longest side, or bottom, is of length 7. Let’s try.
Note the 30 degree position on the unit circle. Use this line and the x-axis to create a triangle as follows.
Figure 10. Using a circle to find two unknown sides of a 30 degree right triangle.
Unit Circle Quick Lesson
In a circle, each line from the center of the circle to its circumference will have a length of 1. Therefore, the longest side of this triangle will have a length of 1. The longest in a right triangle is also called the “hypotenosis”. The point of contact of the bottom with the circumference of the circle is at √3/2, 1/2.
So we know that the base of the triangle (on the x-axis) has a length of √3/2 and the height of the triangle is 1/2.
Another way to think about it is that the base is 3/2 the length of the bottom and the height is 1/2 the length of the bottom.
Unit Circle Diagrams
Therefore, if the length of the hypotenuse is 7, the base of the triangle is 7 x √3/2 = 7√3/2. The height of the triangle will be 7 x 1/2 = 7/2.
Antivirus software deals from HowStuffWorks and TotalAV Security Try Crosswords! Can you solve this riddle? Calculate the coordinates of a point on a circle whose central angle is in radians or degrees. You will get the sine, cosine and tangent of the result.
A unit circle is a circle with a radius equal to 1 and
Tikz Unit Circle
Unit circle trig functions chart, unit circle chart trig, unit-circle, sin cos tan unit circle chart, unit circle chart all six trig functions, completed unit circle chart, full unit circle, unit circle, unit circle chart radians, trigonometric unit circle chart, unit circle table chart, unit circle chart pdf
Related For Full Unit Circle Chart
Free Haccp Plan Template
Free Haccp Plan Template. I agree to receive occasional
Examples Of Meeting Agendas Templat
Examples Of Meeting Agendas Templates. Persons attending the meeting
Past Due Letter
As of the date of this letter, there is